Kohn-Sham random-phase approximation
This chapter describes three different programs that are related to Kohn-Sham based RPA correlation methods. The first one is the density fitting RPA program of Heßelmann et al. described in section Density fitting RPA programs. The second one is the RPATDDFT program by Toulouse et al., see section Random-phase approximation (RPATDDFT) program. And finally section Self consistent RPA programs presents a set of programs which can be used to perform self consistent EXX and RPA calculations developed by Trushkin and Görling.
All of the different codes are capable to perform standard RPA correlation energy calculations, but have distinct features which separate them from each other. More details about each program's capabilities can be found in the respective subsections.
Density fitting RPA programs
Electron correlation energies within the random-phase approximation can be calculated by the programs DIRPA, RPAX2 and ACFDT that are subdirectives of the driver command KSRPA. These methods should be used in conjunction with Kohn-Sham reference determinants, i.e., orbitals and orbital energies from a preceeding DFT calculation should be supplied. An alterntive implementation of various RPA electron correlation methods by Julien Toulouse and co-workers is described in the subsection Random-phase approximation (RPATDDFT) program. The second alternative implementation of RPA is based on the adiabatic-connection fluctuation-dissipation and is described in the subsection RIRPA program. This implementation additionally allows calculations with σ-functionals, which at negligible computational cost significantly improves over RPA in the calculation of various chemical properties.
The self-consistent random phase approximation method (J. Chem. Phys. 139, 084113 (2013), Phys. Rev. Lett. 134, 016402 (2025)) is implemented in the SCRPA program. The program uses the optimized effective potential method to construct the exact exchange potential and the random phase approximation correlation potential. The SCEXX program offers the self-consistent exact exchange optimized effective potential method (J. Chem. Phys. 127, 054102 (2007), J. Chem. Phys. 155, 054109 (2021)) that neglects correlation.
A typical input to calculate the RPAX2 correlation energy is given by:
basis={
set,orbital; default,<basis>
set,mp2fit; default,<basis>/mp2fit}
ks,pbe
{ksrpa; rpax2,orb=2100.2}
All methods are implemented using density-fitting of the two-electron repulsion integrals, see Refs. [2,4]. Because of this, auxiliary basis sets for fitting occupied-virtual orbital pairs have to be given, see section auxiliary basis sets for density fitting or resolution of the identity. No point-group symmetry can be used for all methods described in this section.
References:
RPA:
$[1]$ F. Furche, Phys. Rev. B 64, 195120 (2001).
RPAX2:
$[2]$ A. Heßelmann, Phys. Rev. A 85, 012517 (2012).
$[3]$ A. Heßelmann, Top. Curr. Chem. 365 97 (2015)
ACFDT(ALDA):
$[4]$ A. Heßelmann and A. Görling, J. Chem. Theory Comput. 9, 4382 (2013).
DIRPA program
The direct RPA program (implemented with the algorithm described in [1]) has the following options:
- ORB record number containing the orbital coefficients and eigenvalues (mandatory)
- AUXBAS string containing the label for the auxiliary basis set (default
MP2FIT) - CORE number of core orbitals (which are not correlated)
- MAXIT maximum number of iterations (default ’40’)
- THREN threshold for convergence of energy (default ’1d-8’)
- FMIX mixing factor for the amplitude update $T^{\text{new}}=f T^{\text{old}}+(1-f)T^{\text{new}}$ (default: ’0.4d0’)
- RESTART logical flag to enable a restart from an unfinished calculation. For this, the 3-index Coulomb integrals (Lc.dat) and the two amplitude files (T0.dat and T1.dat) are required if MODE=1 or MODE=2, see below. In case of MODE=3, Molpro’s file 4 needs to be saved in the previous calculation (using, e.g.,
file,4,rpa.datat the beginning of the input file) (default: ’0’) - NOMAX maximum number of $N_{\text{aux}}\times N_{\text{virt}}$ batches to be kept in memory ($N_{\text{aux}}$: number of auxiliary basis functions, $N_{\text{virt}}$: number of virtual orbitals). (assumes: MODE=1, default: ’50’)
- MODE can have the values ’0’,’1’,’2’ and ’3’. If MODE=0 all 3-index quantities are kept in memory. If MODE=1, external 3-index integral and amplitude files are written (to the wavefunction directory). With MODE=2 larger batches of amplitudes can be read/written as specified with NOMAX. MODE=3 is a duplicate of MODE=1, but the 3-index quantities are written to an internal Molpro file (default: ’MODE=3’)
- L string containing the scratch file name for the 3-index Coulomb integrals (default: ’Lc.dat’)
- T0 string containing the scratch file name for the amplitudes (default: ’T0.dat’)
- T1 string containing the scratch file name for the amplitude updates (default: ’T1.dat’)
- SOSEX logical flag, set to SOSEX=1 if the SOSEX energy shall be calculated after convergence (default: ’SOSEX=0’)
Note that in case of MODE=1 or MODE=2 it is recommended to have the wavefunction (wfu) directory located on a scratch partition. E.g., add the command line option -W /scratch/$USER/wfu to the Molpro command.
RPAX2 program
The RPAX2 method is an extension to the RPA and accounts for higher order particle-hole pair exchange contributions [2,3]. The RPAX2 program has the same options as the DIRPA program, see section DIRPA program. The following list shows a few additional ones that can be used:
- DIR if set to DIR$\ne$0 this enables a direct RPA calculation (default ’0’)
- MEM if set to MEM$\ne$0 the 3-index Coulomb integrals and the amplitudes are kept in memory (default: 0)
Spin-unrestricted calculations can be done using the URPAX2 program. In this case the orbitals from a preceeding unrestricted Kohn-Sham calculation have to be passed to the program (via the ORB key).
ACFDT program
The ACFDT (adiabatic connection fluctuation-dissipation theorem) method is an alternative approach to derive the RPA. If used in conjunction with local adiabatic exchange-correlation kernels, the method can also describe electron-electron interaction contributions beyond the RPA. Currently, the ALDA xc-kernel can be used in the program (ACFDT(ALDA) method), see also Ref. [4]. The ACFDT program has the following options:
- ORB record number containing the orbital coefficients and eigenvalues (mandatory)
- AUXBAS string containing the label for the auxiliary basis set (default
MP2FIT) - CORE number of core orbitals (which are not correlated)
- NFREQ number of frequency quadrature points (default ’20’)
- NCOUP number of coupling strength quadrature points (default ’7’)
- GRIDTHR threshold for grid accuracy (default ’1d-10’)
- THRKERN threshold for density in kernel integration (default ’1d-12’)
- XFAC factor tor ALDA exchange contribution (default ’1d0’)
- CFAC factor tor ALDA correlation contribution (default ’1d0’)
- NOXC can be set to ’NOXC$\ne 0$’ if no ALDA xc-contribution shall be added to the electron-electron interaction (which then corresponds to a standard direct RPA calculation) (default ’0’)
- OMQUAD set to ’1’ for Gauss-Chebyshev quadrature and ’2’ for Gauss-Legendre quadrature (default ’2’)
- W0 parameter for Gauss-Legendre quadrature, see R. D. Amos et al., J. Phys. Chem. 89 (1985) 2186
- L3ALPHA logical flag to switch on calculation of coupling-strength dependent xc-kernel integrals (deactivated by default)
- FXC2IDX logical flag for performing a double density fitting approximation of the electron-electron interaction matrix (deactivated by default)
- FXC2 a switch for various approaches to calculate the 2-index xc-kernel integrals (default ’1’)
- THRDUM threshold for density on dummy centre quadrature points (if set to a large value, the dummy centre quadrature points are skipped completely) (default ’0d0’)
- SING logical flag to enable handling of singularity of 2-index xc-kernel integrals, see also the following two options (enabled by default)
- ESHIFT corresponds to $\epsilon$ in $f=1-\rho/(\rho+\epsilon)$ (default: ’1d-5’)
- FSCAL corresponds to $s$ in $\rho=\rho+s\cdot f$ (default ’1d-4’)
The ACFDT(ALDA) method is ill-defined for short electron-electron distances, see Ref. [4] and F. Furche and T. Van Voorhis, J. Chem. Phys. 122, 164106 (2005). Because of this, the method does not have a defined basis set limit and the ACFDT program should not generally be used to calculate ACFDT(ALDA) correlation energies. Instead, the ACFDT2 should be utilised which implements the hybrid approach as described in Ref. [4] and which has, in addition to the ones given above, the following options:
- SCAL scaling factor for the RPA kernel (used for short electron-electron distances) (default ’1d0’)
- MU range-separation parameter. If not used, the program does not perform a correction for the short range electron-electron interaction.
For applying the correction as described in Ref. [4], the vaules of SCAL and MU have to be set to the values SCAL=0.6 and MU=2d0.
The ACFDT3 program implements an approximation to the ACFDT(ALDA) method assuming that the xc-kernel matrix depends linearly on the coupling strength (which is true for the exchange contribution but not, in general, for the correlation contribution to the kernel). Within this approximation the coupling-strength integration can be done analytically leading to a performance improvement over the ACFDT and ACFDT2 programs. The options for ACFDT3 are identical to the ones given above for ACFDT and ACFDT2.
Random-phase approximation (RPATDDFT) program
The random-phase approximation program (rpatddft) can be used to calculate RPA correlation energies after a SCF calculation. Additionnally, it can be used to calculate dynamic dipole polarizabilities, C$_6$ dispersion coefficients, and excitation energies. The program currently works without point-group symmetry.
List of the main keywords:
ECORR, <list of methods>
Calculation of RPA correlation energies [1] (see options below)
PROPERTIES, <list of methods>
Calculation of dynamic dipole polarizabilities and C$_6$ dispersion coefficients [10] (see options below)
EXCIT, <list of methods>
Calculation of excitation energies [11] (see options below)
ORB,<orbrec>Record for input orbitals (required).
as well as contextual options (see later for an explanation on this):
INTAC,NLAMBDA=<n>[,LAMBDA=<lambda>,WEIGHT=<weight>]
Number of quadrature points for the Gauss-Legendre numerical integration along the adiabatic connection for RPA calculations (default is 7). If LAMBDA and WEIGHT are given, assumes a one-point quadrature with given abscissa and weight.
INTFREQ,METHFREQ=<methfrq>,NFREQ=<nfreq>
Options for the numerical integration over the frequency variable of RPA calculations. METHFREQ governs the type of quadrature used (0(default) is Gauss-Chebyshev, 1 and 2 are Gauss-Legendre, 3 is Clenshaw-Curtis) and NFREQ governs the number of quadrature points (default is 16).
DIELMODE,modeUse the solid-state variant when performing DIEL calculations.
and global options, shared by all commands inside the rpatddft block:
STABCheck matrices stability conditions in RPA calculations. When used without anECORR,EXCITorPROPERTIESkeyword, check the Hessian and RPA matrices eigenvalues and do nothing more.DFTKERNEL,<funcx>[,<funcc>]
Specify the exchange and correlation kernel for EXCIT (if only one argument is given, it is understood to be the exchange-correlation kernel).
C6Computes C6 coefficients from last two saved polarizabilities.TDATamm-Dancoff approximation forEXCITandPROPERTIES.NOMP2The MP2 energy is calculated in certain situations where it is available almost for free, provided that some matrices are allocated. This behavior can be switched off by thisNOMP2keyword.NOSPINBLOCKFor spin-unrestricted calculations, use a formalism where matrices are of $\alpha\alpha+\alpha\beta+\beta\alpha+\beta\beta$ dimensions (the default is to use a formalism with a nospinflip/splinflip block structure)NOSPINFLIPExclude spin-flip dimensions of unrestricted RPA calculations that use theNOSPINBLOCKformalism (not suitable for all RPA variants).WRITEFILEWrite files with eigenvalues, virtual orbital energies, dipole moments, dipole velocities, dipole accelerations and amplitudes from a TDA calculationVIAXPY#to comment#INTEGRAL,<nbr>Specify the two-electron integral transformation routine: 0 (still the default for spin-unrestricted and gradient calculations) is the ‘old’ one, 1 is the ‘old’ one that has been cleaned up, and 2 (default otherwise) is a much more efficient transformation using Molpro’stransformroutine.OCC,<nocc>Explicitly specify the number of occupied orbitals (useful for fake pseudopotential calculations).CORE,<core>Specify core orbitals (default: last specified core orbitals or, if none, atomic inner shells)PRINT,<nbr>Level of print expected from the output (from 0(default) to 3).PRINT_INT,<nbr>Level of print of integrals (AO,MO,Orbtials,…), from 0 to 4.PRINT_TIME,<nbr>If greater or equal to 1, will print out information on time spent in routines.
Calculation of RPA correlation energies ECORR, <list of methods>
If no method is given, a SO2-RCCD calculation will be done (see below).
There are two main RPA variants [1]: dRPA (direct RPA, without the inclusion of an Hartree-Fock exchange kernel in the response function) and RPAx (with the Hartree-Fock exchange kernel included in the response function).
There are four main formulations in which the RPA equations can be derived. The adiabatic-connection fluctuation-dissipation theorem (ACFDT) equation involves integrations both over frequency and coupling constant: an analytical integration along the frequency variable followed by a quadrature on the coupling constant yields the adiabatic connection formulation (AC) [1], while an analytic integration on the coupling constant followed by a numerical integration over the frequency yields the dielectric formulation (DIEL) [2]. Two other formulations are obtained when the two integrations are carried out analytically: the plasmon formula (PLASMON) [1] and the ring coupled cluster doubles formulation (RCCD) [3]. These four formulations are not in general equivalent.
Most variants+formulations can readily by used in a spin-unrestricted context [6]. This is implemented in the code and does not need any further input from the user: the RPA program recognizes the spin-unrestricted character of a SCF calculation that was done beforehand and acts accordingly.
Gradients of most of the RCCD-formulation RPA energies are available, both without range-separation with RHF orbitals and with range-separation with RSH orbitals [9]. The calculations are triggered by the presence of the keyword FORCE or OPTG after the energy-related section (see examples at the end of the section).
The user can test the RPA program using make rpatddfttest, which proposes a variety of tests for RPA correlation energy calculations.
The keywords for the methods are constructed on the model:
<variant>-<formulation>-<alternative>
For the AC formulation, the available methods are:
DRPAI-ACdRPA calculation (see Refs. [1] and [4]).DRPAII-ACdRPA calculation, using antisymmetrized two-electron integrals (see Refs. [1] and [4]).RPAXI-ACRPAx calculation (see Refs. [1] and [5]).RPAXII-ACRPAx calculation, using antisymmetrized two-electron integrals (see Refs. [1] and [5]).DRPAI-AC-ALTdRPA calculation using an alternative derivation (see Ref. [7]).RPAXI-AC-ALTRPAx calculation using an alternative derivation (see Ref. [7]).DRPAI-AC-NOINTdRPA calculation without integration along the adiabatic connection (using the “kinetic” and “potential” contributions, sometimes called the “alternative plasmon formula”, see Ref. [1]).RPAXII-AC-NOINTRPAx calculation without integration along the adiabatic connection (using the “kinetic” and “potential” contributions, sometimes called the “alternative plasmon formula”, see Ref. [1]).
For the DIEL formulation, the available methods are:
DRPAI-DIELdRPA calculation (see Ref. [2]).DRPAIIA-DIELdRPA-IIa approximation (see Ref. [2]).RPAXIA-DIELRPAx-Ia approximation (see Ref. [2]).
For the RCCD formulation, the available methods are:
DRPAI-RCCDdRPA-I calculation (see Ref. [3]).RPAXII-RCCDRPAx-II calculation (Szabo-Ostlund variant 1 is calculated too, see Ref. [3]).SO2-RCCDSzabo-Ostlund variant 2 (see Ref. [3]).SOSEX-RCCDdRPA-I+SOSEX correction (see Ref. [3]).RPAX2-RCCDRPAX2 approximation (see Ref. [8]).
For the PLASMON formulation, the available methods are:
DRPAI-PLASMONdRPA-I calculation (see Ref. [1]).RPAXII-PLASMONRPAx-II calculation (see Ref. [1]).
Note that to all these keywords are associated energy variables defined as :
ECORR_VARIANT_FORMULATION_ALTERNATIVE
(see the examples below).
Example of a dRPA-I calculation using the PBE functional:
{rks,pbe,orbital,2101.2}
{rhf,start=2101.2,maxit=0}
{rpatddft;
orb,2101.2;
ecorr,DRPAI-AC
}
e=ECORR_DRPAI_AC
Example of a range-separated RPAx-I calculation using the short-range PBE exchange-correlation functional and the range-separated parameter mu=0.5:
{int;erf,0.5}
{rks,exerfpbe,ecerfpbe;rangehybrid;orbital,2101.2}
{rpatddft;
orb,2101.2;
ecorr,RPAXI-AC
}
Example of several RPA calculations in the same run:
{rhf,orbital,2101.2}
{rpatddft;
orb,2101.2;
ecorr,DRPAI-AC,RPAXII-RCCD,DRPAI-DIEL
}
e1=ECORR_DRPAI_AC
e2=ECORR_RPAXII_RCCD
e3=ECORR_DRPAI_DIEL
(this way, the calculations are done with the same transformed integrals, i.e. without redoing the integral transformation).
Example of a dRPA-I gradient calculation:
{rks,pbe,orbital,2101.2}
{rpatddft;
orb,2101.2;
ecorr,DRPAI-RCCD
}
force
Example of a geometry optimization at the LDA+dRPA-I level:
{int;erf,0.5}
{rks,exerf,ecerf;rangehybrid;orbital,2101.2}
{rpatddft;
orb,2101.2;
ecorr,DRPAI-RCCD
}
optg
Calculation of properties, excitation energies and oscillator strengths
EXCIT, METHOD=<method> The EXCIT calculations output shows the excitation energies in ua, eV and nm, the oscillator strengths in length and velocity gauge, as well as the major excitations involved in each mode. The methods available are:
DRPADirect random-phase approximation (or time-dependent Hartree).TDHFTime-dependent Hartree-Fock.TDDFTTime-dependent density-functional theory.RS-TDDFTRange-separated time-dependent density-functional theory [11].
The exchange density functionals (FUNCX) available are:
LDAXERF(short-range LDA exchange density functional for the erf interaction [12]).
The correlation density functionals (FUNCC) available are:
LDAC(Perdew-Wang-92 LDA correlation density functional)LDACERF(short-range LDA correlation density functional for the erf interaction [13]).
Example of a range-separated time-dependent density-functional theory calculation using the short-range LDA exchange-correlation functional and the range-separated parameter mu=0.5:
mu=0.5
{int;erf,mu;save}
{rks,exerf,ecerf;rangehybrid;orbital,2101.2}
{int}
{setmu,mu}
{rpatddft;
orb,2101.2;
excit,method=rs-tddft;
dftkernel,funcx=ldaxerf,funcc=ldacerf
}
Example of a TDHF-TDA calculation with writing of several files for interfacing with a real-time propagation code (see Ref. [14]):
{rpatddft;
integral,1;
writefile,transmom.dat,energies.dat,virtual.dat,transmom_v.dat,amplitudes.dat,transmom_a.dat;
orb,2330.2;
excit,method=tdhf;
NOSPINBLOCK;
tda}
The files are: transmom.dat: transition moments in position form; energies.dat: total energies of the states; virtual.dat: virtual positive-energy orbitals; transmom_v.dat: transition moments in velocity form; amplitudes.dat: coefficients of excited-state wave functions over single-excited determinants; transmom_a.dat: transition moments in acceleration form
References
$[1]$ J. G. Ángyán, R.-F. Liu, J. Toulouse, and G. Jansen, J. Chem. Theory Comput. 7, 3116 (2011).
$[2]$ G. Jansen, B. Mussard, D. Rocca, J. G. Ángyán (in prep).
$[3]$ J. Toulouse, W. Zhu, A. Savin, G. Jansen, and J. G. Ángyán, J. Chem. Phys. 135, 084119 (2011).
$[4]$ F. Furche, Phys. Rev. B 64, 195120 (2001).
$[5]$ J. Toulouse, I. C. Gerber, G. Jansen, A. Savin, and J. G. Ángyán, Phys. Rev. Lett. 102, 096404 (2009).
$[6]$ B. Mussard, P. Reinhardt, J. G. Ángyán, and J. Toulouse, J. Chem. Phys. (submitted).
$[7]$ Heßelmann, A., Görling, A., Phys. Rev. Lett. 106, 093001 (2011).
$[8]$ Heßelmann, A., Phys. Rev. A 85, 012517 (2012).
$[9]$ B. Mussard, P. G. Szalay, J. G. Ángyán, J. Chem. Theory Comput. 10, 1968 (2014).
$[10]$ J. Toulouse, E. Rebolini, T. Gould, J. F. Dobson, P. Seal, J. G. Ángyán, J. Chem. Phys. 138, 194106 (2013).
$[11]$ E. Rebolini, A. Savin, J. Toulouse, Mol. Phys. 111, 1219 (2013).
$[12]$ J. Toulouse, A. Savin, and H.-J. Flad, Int. J. Quantum Chem. 100, 1047 (2004).
$[13]$ S. Paziani, S. Moroni, P. Gori-Giorgi, and G. B. Bachelet, Phys. Rev. B 73, 155111 (2006).
$[14]$ E. Coccia, B. Mussard, M. Lebeye, J. Caillat, R. Taieb, J. Toulouse, and E. Luppi, Int. J. Quant. Chem. 116, 1120 (2016).
Self consistent RPA programs
RIRPA program
The RIRPA and URIRPA programs allow non-self-consistent spin-restricted and spin-unrestricted resolution of identity (RI) random phase approximation (RPA) [1-3] and σ-functional [4-6] calculations. These methods should be used in conjunction with conventional Kohn-Sham (KS) density functional theory (DFT) calculations, i.e. data from a preceding KS DFT calculation should be provided. Conventional KS DFT means calculations with LDA, GGA and hybrid exchange-correlation functionals.
Bibilography:
RPA:
[1] F. Furche, Phys. Rev. B, 195120 (2001)
[2] A. Heßelmann and A. Görling, Mol. Phys. 109, 2473 (2011)
[3] X. Ren, P. Rinke, C. Joas, and M. Scheffler, J. Mater. Sci. 47, 7447 (2012)
σ-functionals:
[4] E. Trushin, A. Thierbach, A. Görling, J. Chem. Phys. 154, 014104 (2021)
[5] S. Fauser, E. Trushin, C. Neiss, A. Görling, J. Chem. Phys. 155, 134111 (2021)
[6] C. Neiss, S. Fauser, A. Görling, J. Chem. Phys. 158, 044107 (2023)
Other papers cited in the documentation:
[7] E. Trushin, A. Görling, J. Chem. Phys. 155, 054109 (2021)
We kindly ask you to cite the original publications of the corresponding methods in the publications that result from these programs.
Example input file for spin-restricted calculations for the CO molecule:
- examples/co_rirpa.inp
gthresh,twoint=1d-20,energy=1d-10,orbital=1d-8 ! tighter thresholds are recommended gdirect ! integral-direct mode basis={ default,aug-cc-pwCVQZ ! orbital basis set,ri; default,aug-cc-pwCVQZ/mp2fit ! RI basis } symmetry,nosym ! RIRPA does not use symmetry angstrom geometry={ 2 C 0.000000 0.000000 -0.646514 O 0.000000 0.000000 0.484886 } df-ks,pbe,df_basis=aug-cc-pwCV5Z/mp2fit,maxit=200 ! DFT calculation {cfit,basis_coul=aug-cc-pwCV5Z/mp2fit,basis_exch=aug-cc-pwCV5Z/mp2fit} acfd;rirpa ! RPA/sigma-functional calculation; one can use alternatively: ksrpa;rirpa
As well as an example of spin-unrestricted calculation for the NH2 molecule:
- examples/nh2_urirpa.inp
gthresh,twoint=1d-20,energy=1d-10,orbital=1d-8 ! tighter thresholds are recommended gdirect ! integral-direct mode basis={ default,aug-cc-pwCVQZ ! orbital basis set,ri; default,aug-cc-pwCVQZ/mp2fit ! RI basis } symmetry,nosym ! URIRPA does not use symmetry angstrom geometry={ 3 N 0.000000 0.000000 0.142235 H 0.000000 0.800646 -0.497821 H 0.000000 -0.800646 -0.497821 } spin=1 df-uks,pbe,df_basis=aug-cc-pwCV5Z/mp2fit,maxit=200 ! DFT calculation {cfit,basis_coul=aug-cc-pwCV5Z/mp2fit,basis_exch=aug-cc-pwCV5Z/mp2fit} acfd;urirpa ! RPA/sigma-functional calculation; one can use alternatively: ksrpa;urirpa
The following options are available for the RIRPA and URIRPA programs:
- orb record number containing the orbital coefficients, eigenvalues, etc. from the preceding DFT calculation (default: ‘2100.2’ and ‘2200.2’ for RIRPA and URIRPA, respectively)
- dfit logical flag to enable density fitting during the reference energy calculation (default: ’1’)
- sigma logical flag to enable σ-functional calculation (default: ’1’)
- sigma_param string containing a name for the parametrization used (default depends on exchange-correlation functional used in preceding DFT calculation: ‘PBE_S1’ [6] for PBE, ‘PBE0_S1’ [6] for PBE0, ‘TPSS_W1’ [5] for TPSS, ‘B3LYP_S1’ [5] for B3LYP)
- write_sigma logical flag to enable writing of sigma.dat file with reference energy, frequency integration weights and σ-values (default: ’0’)
- thr_overlap_ri threshold for processing RI basis according to Section IIB2 in Ref. [7] (default: ‘1d-99’)
- thr_fai_ri threshold for processing RI basis according to Section IIB5 in Ref. [7] (default: ‘1d-14’)
- thr_rpa threshold for throwing out contributions corresponding to small eigenvalue differences during construction of the response function (default: ‘1d-6’)
- nquadint number of logarithmically spaced intervals for frequency integration (default ‘1’)
- nquad number of points per interval for frequency integration (default '50')
- w0 scaling factor for the rational function mapping the Gauss–Legendre quadrature for the interval [−1, 1] to the interval [0, ∞], see Eqs. 37-38 in Ref. [4] for details (default: ‘2.5’)
- vc_scal scaling factor for the Coulomb kernel, which can be used to mimic the effect of the inclusion of the exact-exchange kernel. In the special case of non-spin-polarized two-electron systems, the RPA calculation with a Coulomb kernel scaled by 1/2 is equivalent to including of the exact-exchange kernel. Implemented only in RIRPA (default: ‘1d0’)
- verb determines the level of verbosity in the output file, integer values of 0, 1, 3 provide different levels of verbosity (default ’0’)
SCEXX program
The SCEXX and USCEXX programs allow self-consistent exact-exchange calculations for closed-shell and open-shell systems.
Bibilography:
[1] A. Heßelmann, A.W. Götz, F. Della Sala, A. Görling J. Chem. Phys. 127, 054102 (2007)
[2] E. Trushin, A. Görling, J. Chem. Phys. 155, 054109 (2021)
[3] E. Trushin, A. Görling, J. Chem. Phys. 159, 244109 (2023)
[4] P. Bleiziffer, A. Heßelmann, A. Görling J. Chem. Phys. 139, 084113 (2013)
NOTE: We have tutorial which provides practical Hands-on examples about the use of SCEXX and USCEXX programs and post-processing of results of calculations. This tutorial is a good supplement to this documentation. Link to Tutorial
Important: Read carefully the information below about the selection of basis sets and the thr_fai_oep parameter:
To obtain numerically stable exchange potentials, one must either use regularization techniques to carefully handle the small eigenvalues of the response matrix or to use auxiliary basis sets that are balanced to the orbital basis set. The latter can be done by manually constructing specific orbital and auxiliary basis sets that are sufficiently balanced. This has been possible for a number of atoms and molecules with quite large orbital basis sets [1], but does not qualify as a general applicable routine approach. The SCEXX and USCEXX programs therefore contain a new preprocessing scheme for auxiliary basis sets that effectively removes linear combinations of auxiliary basis functions that couple poorly to products of occupied times unoccupied Kohn-Sham orbitals and enable the construction of numerically stable exchange potentials with standard basis sets [2].
The preprocessing step to remove linear combinations of auxiliary basis functions that couple poorly to products of occupied times unoccupied Kohn-Sham orbitals is implemented according to Sec II5 of Ref. [2]. It involves the threshold thr_fai_oep, which determines how many linear combinations of auxiliary basis functions are removed and varies with respect to the size of the orbital basis set used. In Ref. [2], this scheme was tested using Dunning correlation consistent basis sets and recommended thresholds are
| Orbital basis set | thr_fai_oep |
|---|---|
| aug-cc-pwCVTZ | 5e-2 |
| aug-cc-pwCVQZ | 1.7e-2 |
| aug-cc-pwCV5Z | 5e-3 |
These thresholds are expected to work also for orbital basis sets without augmentation cc-pwCVXZ (X=T,Q,5) and without core-polarization functions aug-cc-pVXZ (X=T,Q,5). As an auxiliary basis set (OEP), the aug-cc-pVXZ/mp2fit (X=T,Q,5) family of basis sets works best. In particular, according to Ref. [2], it is recommended to use aug-cc-pVDZ/mp2fit auxiliary basis sets for atoms up to neon and aug-cc-pVTZ/mp2fit auxiliary basis sets for heavier atoms.
The code allows to perform calculations symmetrized in ordinary, spin or both ordinary and spin space according to Ref. [3], see parameters space_sym and spin_sym below.
Below is an example input file for spin-restricted calculations for the CO molecule. Note that the input record from a preceding calculation is mandatory for initialization of orbitals and eigenvalues as starting point for EXX calculation, whereas it can come from HF or DFT calculations with maxit=0.
- examples/co_scexx.inp
gdirect ! integral-direct mode basis={ default,aug-cc-pwCVQZ ! orbital basis set,oep;default,aug-cc-pVDZ/mp2fit ! OEP basis set,dfit;default,aug-cc-pwCV5Z/mp2fit ! density fitting basis } symmetry,nosym ! SCEXX does not use symmetry angstrom geometry={ 2 C 0.000000 0.000000 -0.646514 O 0.000000 0.000000 0.484886 } df-hf,maxit=0,df_basis=dfit ! HF calculation with 0 iteration {cfit,basis_coul=dfit,basis_exch=dfit} acfd;scexx,thr_fai_oep=1.7d-2 ! SCEXX calculation
As well as an example of a spin-unrestricted calculation for the BeF molecule:
- examples/bef_uscexx.inp
gdirect ! integral-direct mode basis={ default,aug-cc-pwCVQZ ! orbital basis set,oep;default,aug-cc-pVDZ/mp2fit ! OEP basis set,dfit;default,aug-cc-pwCV5Z/mp2fit ! density fitting basis } symmetry,nosym ! USCEXX does not use symmetry angstrom geometry={ 2 Be 0.0000000 0.0000000 -0.6823625 F 0.0000000 0.0000000 0.6823625 } charge=0 spin=1 df-uhf,maxit=0,df_basis=dfit ! HF calculation with 0 iterations {cfit,basis_coul=dfit,basis_exch=dfit} acfd;uscexx,thr_fai_oep=1.7d-2 ! USCEXX calculation
The following options are available for the `SCEXX` and `USCEXX` programs:
- orb record from which the orbital coefficients and eigenvalues are read (default: ‘2100.2’ and ‘2200.2’ for
SCEXXandUSCEXX, respectively) - save record in which the resulting orbital coefficients, eigenvalues, etc. are written (default: '2101.2' and '2201.2' for
SCEXXandUSCEXX, respectively) - dfit if set to $\neq$ 0, enable density fitting for two-electron integrals (default: ’1’)
- maxit maximum number of iterations (default '30')
- minit minimum number of iterations (default '3')
- maxdiis maximum size of the DIIS history (default '10')
- fixmix if set to $\neq$ 0, switch from DIIS to linear mixing scheme with fixed mixing ratio. This may be useful for converging systems with a small HOMO-LUMO gap where DIIS may have problems. (default '0')
- mixrate mixing rate for linear mixing scheme, corresponds to the fraction of the old Fock matrix in the new step (default '0.95d0')
- energy threshold for energy convergence (default: '1d-8')
- density threshold for density convergence (default: '0d0')
- thr_sym threshold for symmetrization of the OEP basis set to enforce OEP basis exhibits full symmetry of molecule. Set the threshold to 1d-10 to enable symmetrization. (default: ‘0d0’)
- thr_overlap_oep threshold for processing OEP basis according to Section IIB2 in Ref. [2] (default: ‘1d-99’)
- thr_fai_oep threshold for processing OEP basis according to Section IIB5 in Ref. [2] (default: ‘1.7d-2’)
- thr_oep threshold for throwing out contributions corresponding to small eigenvalue differences appearing in the denominator when constructing the so-called lambda term $1/(\varepsilon_a - \varepsilon_i)$ of the static Kohn-Sham response function (default: ‘1d-6’)
- solve matrix inversion methods to solve the OEP equation. The different options are: GESV, TSVD, GTSVD. GESV corresponds to a direct solution without any regularization technique. TSVD and GTSVD correspond to two solutions with regularization according to Eqs. (55) and (56) of Ref. [4], respectively. (default: 'GTSVD')
- thr_solve threshold used during matrix inversion to solve the OEP equation with TSVD and GTSVD methods. Note that the default threshold of 1d-99 results in the absence of regularization (default: ‘1d-99’)
- vref_fa if set to $\neq$ 0, enable the use of the Fermi-Amaldi potential as reference potential. Otherwise, the reference potential is constructed according to Eq. (45) of Ref. [2] (default: '1')
- vhoep if set to $\neq$ 0, enable the calculation of the Hartree potential from the representation in the OEP basis instead of the construction from the density matrix as in the Hartree-Fock calculation (default: ‘0’)
- space_sym if set to $\neq$ 0, enable the space-symmetrization. When active sets vhoep=1 thr_sym=1d-10. (default: '0d0')
- homo if set to $\neq$ 0, enable the use of the HOMO condition (default '0')
- plot_always if set to $\neq$ 0, enable writing of data-files for plotting for every iteration. Otherwise, only final results are written. (default: '0')
- plot_x if set to $\neq$ 0, enable writing of file with plotting data for exchange potential along x-axis (default: '0')
- plot_y if set to $\neq$ 0, enable writing of file with plotting data for exchange potential along y-axis (default: '0')
- plot_z if set to $\neq$ 0, enable writing of file with plotting data for exchange potential along z-axis (default: '0')
- test_pot if set to $\neq$ 0, enable a numerical test to determine if the potential is the derivative of the energy expression (default ’0’)
- verb determines the level of verbosity in the output file, integer values of 0, 1, 2, and 3 provide different levels of verbosity (default ’0’)
The following parameters are only relevant for the USCEXX program:
- spin_sym if set to $\neq$ 0, enable spin-symmetrization in spin-unrestricted calculations, forcing orbitals and eigenvalues in $\alpha$ and $\beta$ spin channels to be identical (default: ‘0’)
- vref_fa_sameab if set to $\neq$ 0, force the Fermi-Amaldi reference potential to be the same for $\alpha$ and $\beta$ spin channels (default: ‘0’)
Pitfalls:
- One might encounter convergence problem using DIIS for systems exhibiting small HOMO-LUMO gaps. In this case switching to linear mixing scheme often might resolve the problem.
- One might sometimes encounter energy oscillations between two solutions with different numbers of OEP basis functions remaining after OEP basis set preprocessing. A small change in
thr_fai_oepmay solve the problem.
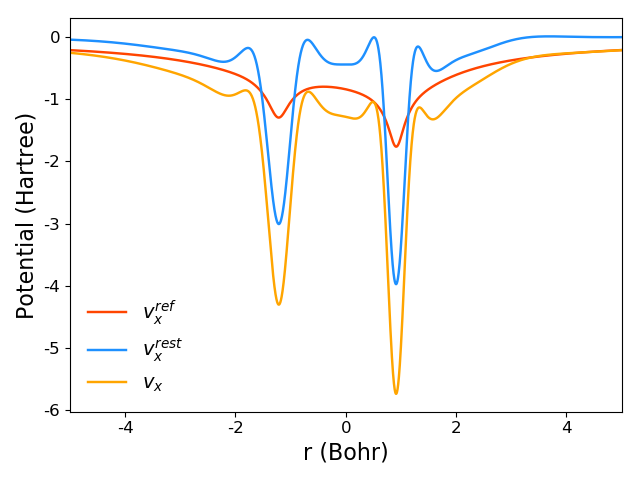
Since the local exchange potential is important in self-consistent exact-exchange calculations, we provide an illustration of how to plot it, including separate contributions. Let us assume that we have performed calculations for CO with the following options:
acfd;scexx,thr_fai_oep=1.7d-2,plot_z=1
At the end there is the file vx-final.z with reference $v_x^{ref}$, rest $v_x^{rest}$ and full $v_x$ exchange potentials. The potentials can be plotted using Python and matplotlib as follows:
import numpy as np import matplotlib.pyplot as plt def load_potential(potfile): """Read data from potential-file. Args: potfile: Path to file with potential data. Returns: x: x coordinate. y: y coordinate. z: z coordinate. coord: coordinate on path. vref: reference potential. vrest: rest potential. v: full potential. """ x, y, z, coord = list(), list(), list(), list() vref, vrest, v = list(), list(), list() for line in open(potfile): aux = line.split() x.append(float(aux[1])) y.append(float(aux[2])) z.append(float(aux[3])) coord.append(float(aux[4])) vref.append(float(aux[6])) vrest.append(float(aux[7])) v.append(float(aux[8])) x, y, z, coord = np.array(x), np.array(y), np.array(z), np.array(coord) vref, vrest, v = np.array(vref), np.array(vrest), np.array(v) return x, y, z, coord, vref, vrest, v _, _, _, coord, vxref, vxrest, vx = load_potential('vx-final.z') plt.plot(coord, vxref, color='orangered', label='$v_{x}^{ref}$') plt.plot(coord, vxrest, color='dodgerblue', label='$v_{x}^{rest}$') plt.plot(coord, vx, color='orange', label='$v_x$') plt.ylabel('Potential (Hartree)', fontsize=16) plt.xlabel('r (Bohr)', fontsize=16) plt.xlim(-5, 5) plt.legend(frameon=False, fontsize=14) plt.tight_layout() plt.show()
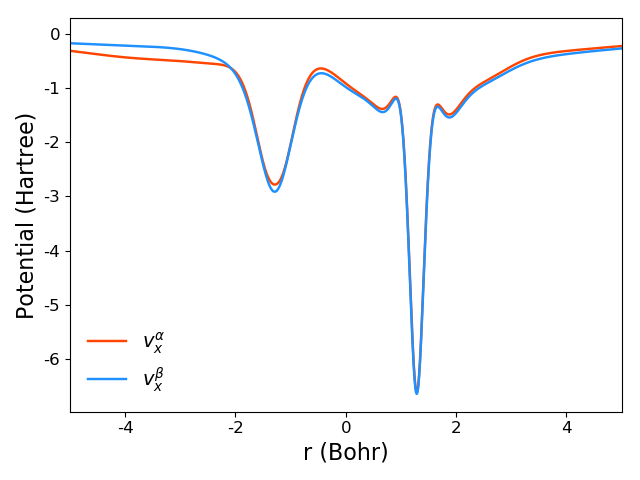
In the similar way, for spin-unrestricted calculations with USCEXX, one ends up with two files vxa-final.z and vxb-final.z with data for $\alpha$ and $\beta$ spin channels, respectively. For BeF one obtains:
import numpy as np import matplotlib.pyplot as plt def load_potential(filename): """Use function from example with CO.""" pass _, _, _, coord, _, _, vxa = load_potential('vxa-final.z') _, _, _, coord, _, _, vxb = load_potential('vxb-final.z') plt.plot(coord, vxa, color='orangered', label=r'$v_{x}^\alpha$') plt.plot(coord, vxb, color='dodgerblue', label=r'$v_{x}^\beta$') plt.ylabel('Potential (Hartree)', fontsize=16) plt.xlabel('r (Bohr)', fontsize=16) plt.xlim(-5, 5) plt.legend(frameon=False, fontsize=14) plt.tight_layout() plt.show()
SCRPA program
The SCRPA and USCRPA programs allow spin-restricted and spin-unrestricted self-consistent random phase approximation calculations.
Bibilography:
[1] A. Heßelmann, A.W. Götz, F. Della Sala, A. Görling J. Chem. Phys. 127, 054102 (2007)
[2] E. Trushin, A. Görling, J. Chem. Phys. 155, 054109 (2021)
[3] P. Bleiziffer, A. Heßelmann, A. Görling J. Chem. Phys. 139, 084113 (2013)
[4] E. Trushin, S. Fauser, A. Mölkner, J. Erhard, A. Görling Phys. Rev. Lett. 134, 016402 (2025)
NOTE: We have tutorial which provides practical Hands-on examples about the use of SCRPA and USCRPA programs and post-processing of results of calculations. This tutorial is a good supplement to this documentation. Link to Tutorial
Important: Read carefully the information below about the selection of basis sets and the thr_fai_oep parameter:
To obtain numerically stable potentials using optimized effective potential method, one must either use regularization techniques to carefully handle the small eigenvalues of the response matrix or to use auxiliary basis sets that are balanced to the orbital basis set. The latter can be done by manually constructing specific orbital and auxiliary basis sets that are sufficiently balanced. This has been possible for a number of atoms and molecules with quite large orbital basis sets [1], but does not qualify as a general applicable routine approach. The SCRPA and USCRPA programs therefore contain a new preprocessing scheme for auxiliary basis sets that effectively removes linear combinations of auxiliary basis functions that couple poorly to products of occupied times unoccupied Kohn-Sham orbitals and enable the construction of numerically stable exchange potentials with standard basis sets [2].
The preprocessing step to remove linear combinations of auxiliary basis functions that couple poorly to products of occupied times unoccupied Kohn-Sham orbitals is implemented according to Sec II5 of Ref. [2]. It involves the threshold thr_fai_oep, which determines how many linear combinations of auxiliary basis functions are removed and varies with respect to the size of the orbital basis set used. In Ref. [2], this scheme was tested using Dunning correlation consistent basis sets and recommended thresholds are
| Orbital basis set | thr_fai_oep |
|---|---|
| aug-cc-pwCVTZ | 5e-2 |
| aug-cc-pwCVQZ | 1.7e-2 |
| aug-cc-pwCV5Z | 5e-3 |
These thresholds are expected to work also for orbital basis sets without augmentation cc-pwCVXZ (X = T, Q, 5) and without core-polarization functions aug-cc-pVXZ (X = T, Q, 5). As an auxiliary basis set (OEP), the aug-cc-pVXZ/mp2fit (X = T, Q, 5) family of basis sets works best. In particular, according to Ref. [2], it is recommended to use aug-cc-pVDZ/mp2fit auxiliary basis sets for atoms up to neon and aug-cc-pVTZ/mp2fit auxiliary basis sets for heavier atoms. As resolution of identity (RI) basis sets aug-cc-pwCVQZ/mp2fit or aug-cc-pwCV5Z/mp2fit basis sets are suitable.
Below is an example input file for spin-restricted calculations for the hygrogen molecule. Note that the input record from a preceding calculation is mandatory for initialization of orbitals and eigenvalues as starting point for RPA calculation, whereas it can come from HF or DFT calculations with maxit=0.
- examples/h2_scrpa.inp
gdirect ! integral-direct mode basis={ default,aug-cc-pwCVTZ ! orbital basis set,ri;default,aug-cc-pwCVQZ/mp2fit ! RI BASIS set,oep;default,aug-cc-pVDZ/mp2fit ! OEP basis set,dfit;default,aug-cc-pwCV5Z/mp2fit ! density fitting basis } symmetry,nosym ! SCRPA does not use symmetry angstrom geometry={ 2 H 0.0 0.0 0.370946 H 0.0 0.0 -0.370946 } df-hf,maxit=0,df_basis=dfit ! HF calculation with 0 iteration {cfit,basis_coul=dfit,basis_exch=dfit} acfd;scrpa,thr_fai_oep=5d-2,plot_z=1 ! SCRPA calculation
As well as an example of a spin-unrestricted calculation for the lithium molecule:
- examples/li_uscrpa.inp
gdirect ! integral-direct mode basis={ default,aug-cc-pwCVTZ ! orbital basis set,ri;default,aug-cc-pwCVQZ/mp2fit ! RI BASIS set,oep;default,aug-cc-pVDZ/mp2fit ! OEP basis set,dfit;default,aug-cc-pwCV5Z/mp2fit ! density fitting basis } symmetry,nosym ! USCRPA does not use symmetry angstrom geometry={ 1 Li 0.0 0.0 0.0 } spin=1 df-uhf,maxit=0,df_basis=dfit ! HF calculation with 0 iteration {cfit,basis_coul=dfit,basis_exch=dfit} acfd;uscrpa,thr_fai_oep=5d-2,plot_z=1 ! USCRPA calculation
The following options are available for the `SCRPA` and `USCRPA` programs:
- orb record from which the orbital coefficients and eigenvalues are read (default: ‘2100.2’ and ‘2200.2’ for
SCRPAandUSCRPA, respectively) - save record in which the resulting orbital coefficients, eigenvalues, etc. are written (default: '2101.2' and '2201.2' for
SCRPAandUSCRPA, respectively) - dfit if set to $\neq$ 0, enable density fitting for two-electron integrals (default: ’1’)
- maxit maximum number of iterations (default '30')
- minit minimum number of iterations (default '3')
- maxdiis maximum size of the DIIS history (default '10')
- fixmix if set to $\neq$ 0, switch from DIIS to linear mixing scheme with fixed mixing ratio. This may be useful for converging systems with a small HOMO-LUMO gap where DIIS may have problems. (default '0')
- mixrate mixing rate for linear mixing scheme, corresponds to the fraction of the old Fock matrix in the new step (default '0.95d0')
- energy threshold for energy convergence (default: '1d-8')
- density threshold for density convergence (default: '0d0')
- thr_sym threshold for symmetrization of the OEP basis set to enforce OEP basis exhibits full symmetry of molecule. Set the threshold to 1d-10 to enable symmetrization. (default: ‘0d0’)
- thr_overlap_oep threshold for processing OEP basis according to Section IIB2 in Ref. [2] (default: ‘1d-99’)
- thr_fai_oep threshold for processing OEP basis according to Section IIB5 in Ref. [2] (default: ‘1.7d-2’)
- thr_oep threshold for throwing out contributions corresponding to small eigenvalue differences appearing in the denominator when constructing the so-called lambda term $1/(\varepsilon_a - \varepsilon_i)$ of the static Kohn-Sham response function (default: ‘1d-6’)
- thr_overlap_ri threshold for processing RI basis according to Section IIB2 in Ref. [7] (default: ‘1d-99’)
- thr_fai_ri threshold for processing RI basis according to Section IIB5 in Ref. [7] (default: ‘1d-14’)
- thr_rpa threshold for throwing out contributions corresponding to small eigenvalue differences during construction of the response function (default: ‘1d-6’)
- solve matrix inversion methods to solve the OEP equation. The different options are: GESV, TSVD, GTSVD. GESV corresponds to a direct solution without any regularization technique. TSVD and GTSVD correspond to two solutions with regularization according to Eqs. (55) and (56) of Ref. [3], respectively. (default: 'GTSVD')
- thr_solve threshold used during matrix inversion to solve the OEP equation with TSVD and GTSVD methods. Note that the default threshold of 1d-99 results in the absence of regularization (default: ‘1d-99’)
- nquadint number of logarithmically spaced intervals for frequency integration (default ‘1’)
- nquad number of points per interval for frequency integration (default '20')
- w0 caling factor for rational the function mapping the Gauss–Legendre quadrature for the interval [−1, 1] to the interval [0, ∞], see Eqs. 37-38 in Ref. [4] for details (default: ‘2.5’)
- vc_scal scaling factor for the Coulomb kernel, which can be used to mimic the effect of the inclusion of the exact-exchange kernel. In the special case of non-spin-polarized two-electron systems, the RPA calculation with a Coulomb kernel scaled by 1/2 is equivalent to including of the exact-exchange kernel. Implemented only in `SCRPA` (default: ‘1d0’)
- vref_fa if set to $\neq$ 0, enable the use of the Fermi-Amaldi potential as reference potential. Otherwise, the reference potential is constructed according to Eq. (45) of Ref. [2] (default: '1')
- vhoep if set to $\neq$ 0, enable the calculation of the Hartree potential from the representation in the OEP basis instead of the construction from the density matrix as in the Hartree-Fock calculation (default: ‘0’)
- space_sym if set to $\neq$ 0, enable the space-symmetrization. When active sets vhoep=1 thr_sym=1d-10. (default: '0d0')
- homo if set to $\neq$ 0, enable the use of the HOMO condition for the exchange potential (default '1')
- plot_always if set to $\neq$ 0, enable writing of data-files for plotting for every iteration. Otherwise, only final results are written. (default: '0')
- plot_x if set to $\neq$ 0, enable writing of file with plotting data for exchange and correlation potentials along x-axis (default: '0')
- plot_y if set to $\neq$ 0, enable writing of file with plotting data for exchange and correlation potentials along y-axis (default: '0')
- plot_z if set to $\neq$ 0, enable writing of file with plotting data for exchange and correlation potentials along z-axis (default: '0')
- test_pot if set to $\neq$ 0, enable a numerical test to determine if the potential is the derivative of the energy expression (default '0')
- verb determines the level of verbosity in the output file, integer values of 0, 1, 2, and 3 provide different levels of verbosity (default '0')
The following parameters are only relevant for the `USCRPA` code:
- spin_sym if set to $\neq$ 0, enable spin-symmetrization in spin-unrestricted calculations, forcing orbitals and eigenvalues in $\alpha$ and $\beta$ spin channels to be identical (default: '0')
- vref_fa_sameab if set to $\neq$ 0, force the Fermi-Amaldi reference potential to be the same for $\alpha$ and $\beta$ spin channels (default: '0')
Pitfalls:
- One might encounter convergence problem using DIIS for systems exhibiting small HOMO-LUMO gaps. In this case switching to linear mixing scheme often might resolve the problem.
- One might sometimes encounter energy oscillations between two solutions with different numbers of OEP basis functions remaining after OEP basis set preprocessing. A small change in
thr_fai_oepmay solve the problem.
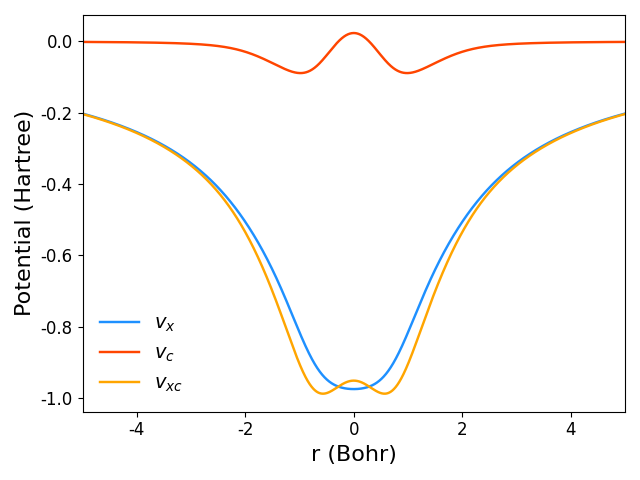
Since the local exchange and correlation potentials are important in self-consistent RPA calculations, we provide an illustration of how to plot these potentials. Let us assume that we have performed calculations for hydrogen molecule with the following options:
acfd;scrpa,thr_fai_oep=1.7d-2,plot_z=1
At the end one has the files vx-final.z with reference $v_x^{ref}$, rest $v_x^{rest}$ and full $v_x$ exchange potentials and vc-final.z with correlation potential. The potentials can be plotted using Python and matplotlib as follows:
import numpy as np import matplotlib.pyplot as plt def load_potential(potfile): """Read data from potential-file. Args: potfile: Path to file with potential data. Returns: x: x coordinate. y: y coordinate. z: z coordinate. coord: coordinate on path. vref: reference potential. vrest: rest potential. v: full potential. """ x, y, z, coord = list(), list(), list(), list() vref, vrest, v = list(), list(), list() for line in open(potfile): aux = line.split() x.append(float(aux[1])) y.append(float(aux[2])) z.append(float(aux[3])) coord.append(float(aux[4])) vref.append(float(aux[6])) vrest.append(float(aux[7])) v.append(float(aux[8])) x, y, z, coord = np.array(x), np.array(y), np.array(z), np.array(coord) vref, vrest, v = np.array(vref), np.array(vrest), np.array(v) return x, y, z, coord, vref, vrest, v _, _, _, coord, vxref, vxrest, vx = load_potential('vx-final.z') _, _, _, coord, _, _, vc = load_potential('vc-final.z') plt.plot(coord, vx, color='dodgerblue', label='$v_x$') plt.plot(coord, vc, color='orangered', label='$v_c$') plt.plot(coord, vx+vc, color='orange', label='$v_{xc}$') plt.ylabel('Potential (Hartree)', fontsize=16) plt.xlabel('r (Bohr)', fontsize=16) plt.xlim(-5, 5) plt.legend(frameon=False, fontsize=14) plt.tight_layout() plt.show()
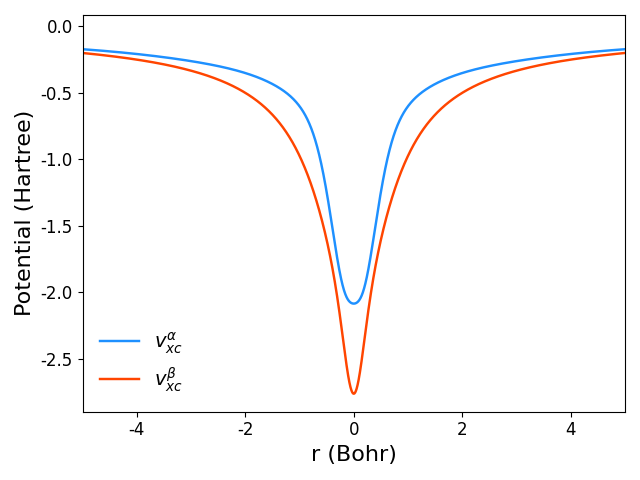
In the similar way, for spin-unrestricted calculations with USCRPA, one ends up with four files vxa-final.z, vxb-final.z, vca-final.z, vcb-final.z with data for $\alpha$ and $\beta$ spin channels. For lithium atom, one can plot, e.g., exchange-correlation potentials for $\alpha$ and $\beta$ spins:
import numpy as np import matplotlib.pyplot as plt def load_potential(potfile): """Use function from example with CO.""" pass _, _, _, coord, _, _, vxa = load_potential('vxa-final.z') _, _, _, coord, _, _, vca = load_potential('vca-final.z') _, _, _, coord, _, _, vxb = load_potential('vxb-final.z') _, _, _, coord, _, _, vcb = load_potential('vcb-final.z') plt.plot(coord, vxa+vca, color='dodgerblue', label=r'$v_{xc,\alpha}$') plt.plot(coord, vxb+vcb, color='orangered', label=r'$v_{xc,\beta}$') plt.ylabel('Potential (Hartree)', fontsize=16) plt.xlabel('r (Bohr)', fontsize=16) plt.xlim(-5, 5) plt.legend(frameon=False, fontsize=14) plt.tight_layout() plt.show()